ХУРМАТ  ХОРЕЗМЕЦ

 

 

 

 

ОДНОВРЕМЕННОСТЬ

И  ЕЕ  РОЛЬ  В  ПОЗНАНИИ ОКРУЖАЮЩЕГО  МИРА

 

 

УРГЕНЧ-2002

 

 

 

 

В книге рассматривается необходимость введения в механику понятия относительных моментов времени и показателя относительной интенсивности течения времени. Это  требуется для осознания роли одновременности в познании окружающего мира. Моменты времени субъекта на поверхности земли переживается им только однажды и последовательные моменты непрерывно протекает только с его точки зрения. Требование непрерывной одновременности отдаленного окружающего связано с определенными условиями. Только выполняющие эти условия объекты окружающего одновременны наблюдателю на протяжении продолжительного времени. Изучения этих условий становится источником знаний о мироустройстве в одновременном относительно центра земли околоземном пространстве.

Книга рассчитана  на преподавателей и студентов ВУЗов занимающихся механикой и теорией относительности.

 

 

ВВЕДЕНИЕ

 

Наши знания становятся ближе к истине и раскроется ложность наших представлений об окружающем мире, после осознания роли одновременности в мироустройстве в пространстве и после оценки степени влияния одновременности на наше познание природы. Считается, что в современной науке достаточно много экспериментально установленных фактов, подтверждающих объективность научных выводов. При формировании знаний о природе меняется истолкования фактов, и в результате этого некоторые факты считаются главными, а некоторые считаются незначительными для научного миропонимания. В разряд незначительных попался, в современной науке, факт относительности моментов времени и связанное с ним понятие одновременности. Относительность момента времени несет в себе понятие одновременного пространства для каждой точки пространства.

Одновременность является глобальным и абсолютным фактором, во-первых, в научном познании окружающего и, во-вторых, в материальном миро устройстве.  Наблюдателя или каждого тела окружает пространство, состоящее из объема, моменты времени в точках которого, одновременны с моментами наблюдателя.  Следовательно, если для наблюдателя существует только одновременное с ним пространство, то одновременность должен стать основным фактором формирующее знания наблюдателя об окружающем. Поэтому исследование показателей, влияющих на одновременность и изучение закономерностей сохранения одновременности, позволяет получить ценные выводы о пространстве вокруг нас и о материальном  устройстве  этого пространства. 

Целью этой работы является описание пространства, сохраняющее одновременность относительно точки наблюдения и исследование условий соблюдения одновременности, в едином пространство - времени, с точки зрения движущегося наблюдателя.

 

 

I.                   ОДНОВРЕМЕННОЕ, ОТНОСИТЕЛЬНО ТОЧКИ  НАБЛЮДЕНИЯ, ПРОСТРАНСТВО

 

Одновременность, основанная на относительности моментов времени точек пространства, отличается от одновременности используемого в современной механике. В классической механике время считалось абсолютной, и при этом существовала  абсолютная одновременность всех точек пространства, без учета относительности моментов времени. Относительность моментов времени несовместима с абсолютным  временем и поэтому это понятие исключалось из рассмотрения в классической механике. Появление теории относительности внесло изменение в понятие “абсолютное время”. Теория относительности выявила ограниченность максимальной скорости распространения любого сигнала и считает, что сигналы, оповещающие о  происхождении  события,  доходят  до  наблюдателя  с конечной скоростью.   Это утверждение делает момент происхождения события относительным по отношению наблюдателя. В результате этого становится невозможным установление одновременности без определения точки пространства, относительно которой устанавливается одновременность. Произвольное установление одновременности приводит к неоднозначным описаниям  происходящего  процесса.  Здесь получается  несоответствие между одновременностью, принятой в классической механике, и, его современным пониманием.  В  механике Ньютона,  когда  время  считалось абсолютной,  не было выделенных, особых точек пространства. Отказ от понятия  "абсолютного времени"  требовало введения понятия ”относительного момента времени”. Это привело бы  внесению больших изменений в механику и пересмотру многих положений классической механики. 

Основоположник теории относительности, А. Эйнштейн, для того чтобы определить одновременность, не используя понятие относительных моментов времени, предлагает синхронизировать часы находящихся в разных точках пространства [8]. Метод синхронизации часов действительно устраняет необходимость введения в механику понятия “относительность моментов времени”. Но, возникает вопрос, уместно ли, замена относительных моментов времени в точках пространства, показаниями воображаемых синхронизированных часов?   

В литературе [1,7] приводится метод синхронизации часов, и по этому методу считается, что путем настройки часов можно добиться одновременности во всех точках пространства. Такой способ достижения одновременности имеет ряд недостатков. Во-первых, момент происхождения процесса связывается с показаниями часов находящихся, в точке происхождения процесса.  При таком методе синхронизации, каждой точке  пространства, рядом с часами,  понадобится свой наблюдатель для регистрации одновременности.  И как результат, здесь исключается возможность наблюдения процесса с точки зрения одного наблюдателя. Следовательно, становится невозможным исследовать и описать одновременного пространства, относительно одного наблюдателя. Во-вторых, при определении момента происхождения события делается предположение об опоздании сигнала на t секунд, прежде чем оно наблюдалось относительно точки наблюдения.  Время  опоздания  сигнала определяется временем преодоления лучом света от объекта до  точки  наблюдения. Скорость луча света не зависит от скорости движения источника света или наблюдателя. Однако, здесь необходимо учитывать изменение времени опоздании сигнала, связанного с перемещением в пространстве, с одной стороны, самой точки происхождения процесса, и с другой стороны, точки наблюдения в пространстве. Метод синхронизации часов не позволяет учитывать влияния этих изменений на установление одновременности. Одним словом,  метод синхронизации часов не может однозначно заменить относительность момента происхождения события.  Проблема в установлении одновременности в современной механике существует и эту проблему нельзя решить только изменением показаний часов. Часы – это инструмент, который отсчитывает число повторяющихся процессов, показание часов в точках происхождения событий, не может указать одновременность событий.  Одновременность это понятие общеприродного масштаба. Одномоментный вид окружающего, относительно точке наблюдения,  может стать примером одновременного состояния  пространства.  При  этом,  положение солнца и звезд,  положение объектов на поверхности земли, состояние исследуемого процесса и показание часов в точке наблюдения должно отражаться в едином, соответствующем друг другу состоянии. Моменты происхождения наблюдаемых вокруг процессов являются относительными с точки зрения времени наблюдения.  Одновременность момента происхождения события и момента в точке наблюдения отмечается наблюдателем относительно своей системы отсчета.  Из этого вытекает определение понятия одновременности: одновременными,  относительно  точке  наблюдения, считаются  такие состояния точек пространства, из которых одновременно поступает  световой  сигнал  наблюдателю, о событиях в этих точках.

В работах [4,5] отмечается отдаленность моментов времени в точках пространства и свойство течения времени связывается с каждой точкой  пространства. Течение  времени  происходит в  каждой точке пространства. При этом моменты времени и интенсивность течения времени в точках различны друг от друга, и зависят от их взаимного расположения в пространстве. До настоящего времени и в науке, и на практике, как эталон, используется только абсолютное и независимое время классической механики. Изменения  всех  параметров рассматривается на фоне изменения времени. Но, независимость и всеобщая роль времени не подтверждена экспериментами. Анализ результатов некоторых опытов показывает зависимость времени от движения. Рассмотрим пример показывающий относительность моментов времени и влияния движения на интенсивность течения времени. Допустим, в пространстве выбрали систему координат, и в этой системе отсчета наблюдаем движение объекта A, направляющегося в точку В. В  начале  системы  координат,  в объекте исследования А и в пункте назначения В установим вращающиеся сигнальные устройства, похожие на

 

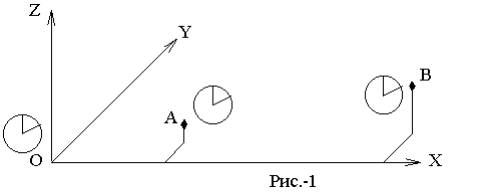
авиационные,  направляющие тонкий световой луч в разные стороны пространства в плоскости вращения. Для отсчета времени частоту вращения устройства в начале отсчета установим на 1 оборот в секунду. Синхронизируем другие устройства таким образом, что к началу отсчета, в объектив на делении 0º,  лучи попадали одновременно. Т.е. обеспечиваем параллельность лучей, исходящих из вращающихся устройств, относительно наблюдателю в начале отсчета. Одновременность поступления сигналов из устройств к точке отсчета указывает на одновременность моментов в точках пространства относительно начала отсчета. И поэтому наблюдатель может считать лучи параллельными с точки зрения своего места нахождения в пространстве. Если объект А движется, то по мере изменения расстояния до точки О, изменяется время поступления сигнала к началу отсчета и синхронность между устройствами  в точках О  и  А, (также  А и В), нарушится. С расстояний  ℓ₁ и ℓ₂ , сигнал  поступает соответственно за время  

              ℓ₁                         ℓ₂      

              t₁ = ––––––,       t₂ = –––––                         (1.1)

                          С                         С

 

Где С  скорость света.

Объект А перемещаясь на Dℓ = ℓ₂ – ℓ₁  должен корректировать свое сигнальное устройство на  Dm   с тем, чтобы остаться одновременным   с устройствами в точках О и В. Величина поправки составляет:

                                           Dℓ

                               Dm = ———                               (1.2)

                                            C

Время объекта А протекает с дополнительной интенсивностью по отношению времени начала отсчета.

            Dt¢ = Dt + Dm                                     (1.3)

Движение в пространстве становится причиной изменения интенсивности течения времени в устройстве регистрации, т.е. в часах, объекта А. Изменение моментов времени происходит не только в результате течения времени, но также и в результате перемещения в пространстве.

 Значит, необходимо найти возможность описать изменения моментов времени в часах движущегося объекта А. Для этого можно учитывать следующие свойства относительного изменения времени. В первую очередь можно найти относительную интенсивность течения времени путем деления величины протекавшего времени в движущемся объекте на промежуток времени в неподвижной точке:

                     Dt + Dm                        Dm

          Kh = ¾¾¾¾¾  =   1+  ¾¾¾                (1.4)

                          Dt                             Dt

 

Или учитывая   (1.2)  имеем:

                             Dℓ            1                        V

          Kh= 1 +  ¾¾¾  · ¾¾  = 1 +   ¾¾¾      (1.5)

                             C             Dt                       C

 

Во-вторых, изменения  моментов времени в движущемся объекте рассматривается как совокупность течения времени и перемещения объекта. Поэтому для оценки величины изменения имеет значение доля каждого изменения  в общем изменении момента времени:

 

        Dt¢ = Dt + Dm                                       (1.6)

 

Из равенства (1.4) получим:

 

           Dt + Dm = Kh · Dt                                (1.7)

 

                Dm = Kh· Dt – Dt = (Kh- 1) · Dt                (1.8)

 

                                         V

 Так как      Kh = ( 1 + ––¾  )                                 (1.9)

                                         C

 

                                      V

Получается:  Dm =  ¾¾ · Dt                                  (1.10)

                                      C      

Пространственная  доля и временная доля в общем течении времени связаны между собой равенством  (1.10).

Предел отношения  Dm  на Dt при Dt® 0 обозначаем буквой H.

 

                  Dm           dm

             ℓ i m   —–— = ——— =   H                                  (1.11)

             Dt®0     Dt           dt

 

 Тогда

                                     V

                        H =  ———                                       (1.12)

                                     C

Или:

                        V             V · t               Dℓ

            H = ———  =  ———  =  ———             (1.13)

                        C               ℓ                   ℓ

 

Из этого равенства можно найти величину наблюдаемого перемещения относительно начала отсчета при движении объекта со скоростью    V.

 

                         V       

             Dℓ = ———  · ℓ = V · t                               (1.14)

                         C       

 

Или разделив на С , Dℓ можно выражать через  Dm:

 

                                     V · ℓ           V  

                        Dm = ——— =  ——— · t               (1.15)

                                      C ²              C

Вышеизложенные равенства (1.14) и (1.15) выражают полную взаимозависимость интенсивности течения времени и движения в пространстве. С одной стороны, движение является причиной возникновения дополнительной интенсивности течения времени, и с другой стороны, дополнительная интенсивность становится причиной возникновения относительного движения. Движение и интенсивность течения времени – это  два проявления одного процесса.

Введение в науку показателя относительной интенсивности течения времени позволяет изучить фундаментальные свойства природы, основывающиеся на взаимосвязанности пространства и времени. Исследование пространства, осознавая относительность моментов времени, и относительность интенсивности течения времени, являются задачей теории одновременности.

Между двумя точками пространства существует расстояние.  На этих точках течет время (т.е. продолжительный подсчет периодически повторяющегося процесса). Одновременность моментов времени в этих точках устанавливается относительно одной из точек (т.е. подсчет периодического процесса в одной точке, может соответствовать подсчету в другой точке относительно одной из точек). Момент времени в одной из точек определяется только относительно другой точке (т.е. подсчет периодического процесса в одной точке можно вести наблюдая из другой точке). Между моментами времени в этих точках есть интервал времени t - показатель выражающий отдаленность моментов времени в этих точках (т.е. показатель выражающий разницу подсчетов в двух точках). Интервал времени между точками определяется скоростью луча света. Скоростью, которая имеет абсолютного предельного значение и максимально быстро может связать моменты времени в точках пространства.  Движение какого то объекта в пространстве есть его перемещение из одной точки в другую. При этом меняется расстояние между объектом и точкой отсчета, относительно которой наблюдается движение объекта. Перемещение объекта сопровождается также изменением интервала времени, отделяющего моменты времени в точке отсчета, относительно которой наблюдается движение, и в объекте наблюдения. Объект, перемещаясь в пространстве, переходит к другой точке, где интервал времени имеет другое значение. Изменение интервала времени влечет за собой изменения соответствующих подсчетов периодического процесса, т.е. времени. Следовательно, изменяется интенсивность течения времени в движущемся объекте (т.е. при подсчете периодического процесса необходимо будет добавить или отнимать дополнительные моменты времени для соблюдения соответствия этих подсчетов, с подсчетами в точке пространства, в котором находится объект). Величина интенсивности течения времени определяется из равенства (1,4), т.е. отношением промежутка времени объекта на время в точке наблюдения (ТН):

                                             Dt_объект

                               Kh = ¾¾¾¾¾                                  (1.16)

                                               Dt_ТН                        

 

или           Dt_объект = Kh · Dt_ТН

 

                                                 V

Где Kh  =  (1 ±  H )  =  1 ±  ——    коэффициент интенсивности 

                                                  C         

течения времени или, то же самое,  коэффициент  нарушения  одновременности. Знак  "±" определяется  направлениями вектора скорости движения объекта и вектора скорости света. Положительным, считается, направление от точки отсчета до объекта, тогда знак получает значение "+", при направлении  скорости  объекта,  в  сторону  увеличения  расстояния, и  знак

"–", в сторону уменьшении расстояния.

Существование дополнительной интенсивности течения времени движущегося объекта нарушает относительность одного к другому. Если один объект движется, относительно другому, неподвижному, то только движущийся объект получает дополнительную интенсивность течения времени. При изменении места наблюдателя,  с неподвижного объекта на движущийся объект,  время наблюдателя на движущемся объекте, окажется с большей интенсивностью, чем время на неподвижном объекте. Это свойство относительного наблюдения в корне изменяет представления, об относительности и о равноправности инерциальных систем отсчета. Коэффициент интенсивности течения времени позволяет отличить движущийся объект, при относительном наблюдении, от неподвижного.  Время движущегося объекта течет быстрее, и объект окажется в относительном будущем по отношении наблюдателя. Промежуток любого процесса наблюдается дольше обычного:   Dt¢ = Dt + Dm . Если наблюдатель находится на движущемся объекте, то время в неподвижном объекте стремится в относительное прошлое. Промежуток времени относительно наблюдателя становится быстропротекающим:  Dt¢ = Dt – Dm.    Процессы протекающие на протяжении времени сравнимые  с   Dm    невозможно будет наблюдать из движущегося объекта. Если какой-то кратковременный процесс происходит на неподвижном объекте, то относительно движущегося наблюдателя этот процесс, не начавшись, окажется в прошлом времени. Не все события пространства одновременны движущемуся наблюдателю. Следовательно, каждой точке движущегося пространства соответствует свое одновременное пространство. Из любой точки движущегося пространства, можно наблюдать только те объекты и события, в которых относительная интенсивность течения времени сравнимы с интенсивностью времени наблюдателя. Изучение условий соблюдения одновременности, во-первых, становится источником знаний о взаимосвязанности пространства и времени, в одновременном относительно центра земли, околоземном пространстве  и,  во-вторых, позволяет осознать существование других, неодновременных, относительно центра земли, пространств.

 

II.                                   УСЛОВИЯ СОБЛЮДЕНИЯ ОДНОВРЕМЕННОСТИ    ОТНОСИТЕЛЬНО ДВИЖУЩЕЙСЯ ТОЧКЕ НАБЛЮДЕНИЯ

 

Движение  нарушает однозначное соответствие состояний объектов. Величина нарушения одновременности определяется из равенства: 

                        V             Dℓ             Dm

             H =  –——  = ——   =   ——–                           (2.1)

                        С              ℓ                t           

Показатель  Н  выражает величину нарушения однозначного соответствия состояния движущегося объекта, относительно другого неподвижного объекта. Моментальному состоянию первого, неподвижного, объекта соответствует последовательность состояний второго, движущегося, объекта из участка пути Dℓ . Моменту времени первого объекта соответствует промежуток времени  Dm  второго объекта. Один объект относительно другому становится моментально реальным в участке пространства  Dℓ  и в промежутке времени Dm . Потому что, сигнал оповещающий о существовании второго  объекта,  исходящий  из  участка  пространства  Dℓ,  доходит до первого объекта одновременно, т.е.  последовательные сигналы доходят в один момент времени.

Наблюдение отдаленного, движущегося,  объекта подчиняется принципу неопределенностей. Одновременно можно наблюдать состояние объекта из отрезка  Dℓ . Если наблюдатель хочет узнать о каждой точке движущегося объекта, то можно получить информацию из промежутка времени Dm , т.е. из некоторой совокупности прошлого и будущего состояний,  этой точки. Собственный момент наблюдателя ограничен текущим временем. Поэтому для достижения однозначного соответствия состояний во времени, т.е. одновременности, наблюдателю необходимо дополнительная интенсивность течения времени равная интервалу времени между объектом и наблюдателем:

                                  Dm · С

                         t = ———–                                      (2.2)

                                     V

Ограниченность возможности наблюдения, из-за нарушения одновременности, можно называть принципом  неопределенности в глобальном масштабе.

Движение объекта, нарушает одновременность не только в окружающем пространстве, но и во внутренних точках объекта. Если объект исследования имеет определенную форму или объем, то каждая точка объекта нарушает одновременность по-разному, т.е. в зависимости от расстояния до центра объекта. Только одна центральная точка объекта движется с коэффициентом интенсивности течения времени:

                                 V_ц

         Kh_ц  =   1 ±  ——                                             (2.3)

                                 С 

Другие точки объекта вокруг центральной точки должны двигаться с разными скоростями V₁, V₂, …., V_n  с тем, чтобы сохранить одновременность относительно центра объекта. Рассмотрим условия соблюдения одновременности относительно движущейся точки наблюдения.  Допустим, точка наблюдения за время   Dt  перемещается в пространстве на расстояние   S   и при этом получает    приращение     во времени:

                                     S

                        Dm = ———                                      (2.4)

                                     C

Всё пространство, чтобы остаться одновременным относительно наблюдателю  в течении этого времени должно получить соответствующие   приращения  Dm_R  во времени. Величина этого приращения зависит от радиуса  R,  окружающего, сохраняющего одновременность относительно точки наблюдения:

                                          R

                         Dm_R  = ——— · Dm                           (2.5)

                                          S

 

Коэффициент             R

                                К_R  = ———                           (2.6)

                                               S

является обратно пропорциональной функцией времени. Но, так как рассматривается условие одновременности на участке пространства радиусом R, то в качестве базового времени, для определения коэффициента, используется время, заложенное, в этом участке пространства, т.е. интервал времени  Dt =t . Для вычисления относительного приращения Dm_R,   необходимого установлению одновременности на радиусе  R,  определяем значение Dm   наблюдателя и значение перемещения S  за время  Dt =t.   Радиус R  делится на S  равные участки, и каждый из этих участков получает по приращению  Dm.   Расстояние S пространства получает приращение Dm,  расстояние 2S  получает приращение 2Dm  и т.д.  расстояние n·S   получает приращение  n·Dm,   где n= R/S .  Участки пространства  S, 2S, n·S  могут получить относительные приращения во времени относительным движением в пространстве. Относительное движение при постоянном радиусе есть вращательное движение вокруг точки наблюдения. Одновременность подобно железным прутьям связывает точки пространства абсолютно жесткой связью. Если одна точка в движущемся со скоростью  V  пространстве перемещается за время t  на расстояние S,  то  окружность в радиусе  S  должна свершить перемещение S + DS,  потому что на расстоянии  S  протекает время t + Dm,  и  S + DS = (t + Dm)·V.  Окружность на расстоянии  2S  совершает перемещение S + 2·DS  и так далее окружность радиусом n·S совершает в пространстве перемещение S + n·DS. или S + DS_R. Необходимость этих перемещений вытекает из условия одновременности пространства относительно наблюдателю, т.е. целостности пространства во времени. Все перемещения точек пространства происходят при постоянных радиусах окружностей, и в плоскостях перпендикулярных к направлению движения или к направлению дополнительного приращения времени Dm, иначе перемещение привело бы неоправданному, беспричинному переходу части одновременного пространства наблюдателя в относительное прошлое или в относительное будущее. 

Основываясь на вышеизложенные условия одновременности можно написать уравнения координат X, Y, Z  движущейся со скоростью V  системы отсчета К',  относительно системы отсчета К. Для упрощения считаем, что оси Х и Х' совпадают, и движение К' происходит по направлению Х. Тогда начало отсчета О' попадает в будущее раньше на Dm в направлении Х относительно точки О.

 

 

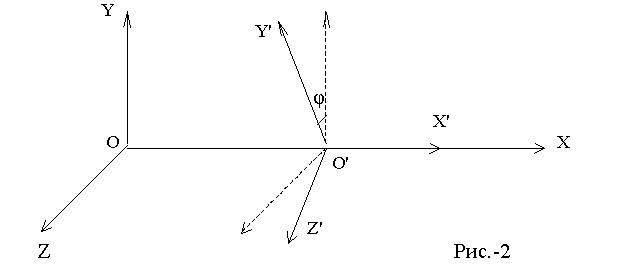
Любая точка оси Х' имеет в системе отсчета К координату X:

 

X = X¢ + V · Dt'                                  (2.7)

 

Точка О' с момента времени t₁ в момент t₂  попадает раньше чем точка О, поэтому

                                                V  

                        Dt¢ = Dt  +  ——— · t                       (2.8)

                                                C

Учитывая значение Dt¢, получим:

 

                                                 V²

               X = X¢ + V · Dt + ——— · t                       (2.9)

                                                 С                               

 

Чтобы соблюдать одновременность относительно О',  точки  осей Y' и Z' получают соответствующие приращения во времени Dm_R и  перемещения DS_R по дуге окружности R. Точки этих осей в системе отсчета К имеют координаты:

 

                    Y  = Y' · cos φ – Z' · sin φ                     (2.10)

                     Z  = Y' · sin φ + Z' · cos φ

 

Где φ -  угол в радианах и по определению φ = DS_R / R.

Соблюдение условий одновременности можно показать на примере околоземного пространства, одновременного относительно центра земли. Центр земли движется в пространстве со скоростью около 30 км/сек. Поверхность земли находится примерно на радиусе 6350 км от центра. Поверхность земли отдалена от центра во времени интервалом t :

 

                         R              6350   

               t =  –––––  =  ––––––– = 0.0211667                 (2.11)

                         С            300000

За время t  центр земли совершает перемещение  S=635м. и получает приращение во времени Dm . Значения этих показателей, и также, величины относительного приращение Dm_R и относительного перемещения DS_R требующееся для установления одновременности в радиусе R с течением времени приведены в таблице 1.

Центр земли, двигаясь в пространстве, нарушает одновременность и переходит к точкам, которые отсутствуют в одновременном пространстве бывшего состояния. Точно также, бывшая пространственно-временная положения центра земли отсутствует в нынешнем одновременном, относительно центра земли, пространстве. За время пока сигнал добирается с поверхности до центра, центр земли проводит в новом, соответствующем скорости V  пространстве, время Dm  и перемещение  DS = V · Dm .    Время  Dm  и  точки расстояния  DS  не принадлежат  бывшему пространству–времени, в котором находился центр земли в прошлом времени.

 

Таблица 1
Показатели одновременности относительно движущегося центра земли
Скорость центра земли V =30000 м/сек, Скорость света: C =300000000 м/сек, Радиус  6350000м
Интервал Dt=t и время  Dt+0.05 сек	V   Dm= —— · t   C	S = V·Dt	R DmR= ––—·Dm              S	DS = V·Dm	R DSR=–—·DS                      S	DSR VR= –––––        Dt
0,02116667	0,0000021167	635	0,0211666667	0,0635	635	30000,0000
0,07116667	0,0000071167	2135	0,0211666667	0,2135	635	8922,7166
0,12116667	0,0000121167	3635	0,0211666667	0,3635	635	5240,7153
0,17116667	0,0000171167	5135	0,0211666667	0,5135	635	3709,8345
0,22116667	0,0000221167	6635	0,0211666667	0,6635	635	2871,1379
0,27116667	0,0000271167	8135	0,0211666667	0,8135	635	2341,7333
0,32116667	0,0000321167	9635	0,0211666667	0,9635	635	1977,1666
0,37116667	0,0000371167	11135	0,0211666667	1,1135	635	1710,8217
0,42116667	0,0000421167	12635	0,0211666667	1,2635	635	1507,7167
0,47116667	0,0000471167	14135	0,0211666667	1,4135	635	1347,7184
0,52116667	0,0000521167	15635	0,0211666667	1,5635	635	1218,4202
0,57116667	0,0000571167	17135	0,0211666667	1,7135	635	1111,7596
0,62116667	0,0000621167	18635	0,0211666667	1,8635	635	1022,2699
0,67116667	0,0000671167	20135	0,0211666667	2,0135	635	946,1137
0,72116667	0,0000721167	21635	0,0211666667	2,1635	635	880,5177
0,77116667	0,0000771167	23135	0,0211666667	2,3135	635	823,4277
0,82116667	0,0000821167	24635	0,0211666667	2,4635	635	773,2900
0,87116667	0,0000871167	26135	0,0211666667	2,6135	635	728,9076
0,92116667	0,0000921167	27635	0,0211666667	2,7635	635	689,3432
0,97116667	0,0000971167	29135	0,0211666667	2,9135	635	653,8528
1,02116667	0,0001021167	30635	0,0211666667	3,0635	635	621,8378

                     

Следовательно, в новое, будущее пространство должно переходить всё одновременное относительно центра земли,  пространство.   Чем дальше объекты от центра, тем быстрее они должны переходить в будущее, с тем, чтобы остаться одновременным относительно центра земли в данный момент. Есть один способ оказаться в будущем быстрее – это движение. Для достижения одновременности окружность на расстоянии  R,  движется относительно центра земли и совершает  перемещение на расстояние:

                                          R

                         DS_R  = ——— · DS                           (2.12)

                                          S

По данным из таблицы 1 величина перемещения  DS_R= 635 м одинаково для разных промежутков времени. Поэтому при определении скорости движения и времени можно использовать следующее равенство:

 

                          Dt' · V' =  Dt'' · V''                             (2.13)

или              

                        1 сек · 635 м/сек  =   t · 30000 м/сек

 

Скорость V' = 635 м/сек.  на расстоянии R от центра может удовлетворить одновременность относительно центра земли. Это соответствует угловой скорости:

 

                 V'                635 м/сек

W  =   ———  =  —————— = 0,0001 сек ^–1        (2.14)   

                  R               6350000 м    

 

Одновременное околоземное пространство должно вращаться вокруг оси течения времени с угловой скоростью W=0,0001сек^–1 . Как известно реальная угловая скорость земли составляет W_з =  0,000073 сек ^–1  . Объект находящийся на поверхности в радиусе  R  вращающийся окружности с этой угловой скоростью получает линейную скорость:       

   

                          V_з  = W_з · R =  463,6 м/сек                   (2.15)

 

Этот скорость объекта несколько меньше скорости, требующейся для достижения одновременности. Земля как будто обратно вращается относительно одновременного пространства с угловой скоростью :

 

                      W_от =  W – W_з = 0,000026 сек ^–1 .

 

Такое состояние объекта на поверхности земли  можно сравнивать с состоянием объекта движущегося со скоростью 463,6 м./сек. внутри корабля, которая имеет скорость 635 м./сек. . Естественно, в этом  случае, объекту необходимо  определенное ускорение, чтобы находиться на одном и том же месте, внутри корабля на длительное время.   Ускорения определяется как отношение величины изменения скорости на время, за которое произошло это изменение.

                             DV          

                а  =   ———                                         (2.16)   

                             D t     

Если  было бы известно значения скорости в двух разных моментах времени, то можно было определить ускорение путем дифференцирования. Когда время в отдаленных от наблюдателя точках  имеет относительную интенсивность течения, то относительные моменты времени необходимо рассматривать как совокупность определенных промежутков времени. Поэтому исключаем время из формулы ускорения используя перестановку:

                  DХ

                Dt   =   ———                                      (2.17)   

                                V_з           

 

Подставляя  (2.17)  в  (2.16) получим формулу для определения ускорения:

 

                                  DV · V_з

                          а  =   —–——                             (2.18)   

                                      Dх

Или        

                     (653-463,5) · 463,5

        а  =   —–——––––––––––                               

                                   DХ

Значение  DХ  выражает величину, не достающегося для достижения одновременности, перемещения, т.е. DХ выражает перемещение относительно одновременному пространству. Относительное, по отношении центра земли, перемещение DS_R= 635м. удовлетворяет одновременность при скорости пространства V=30000 м/сек . Центр земли, вместе с окружающим его пространством, двигаясь с этой скоростью перемещается за 1 сек. на расстояние Х₁=30000м . Скорость пространства соответствующее реальному перемещению DS_з= 467м  определяем из равенства (2.13) :

 

                   1 сек · 463,5 м/сек  =   t ·  V''

 

Отсюда V'' = 21894 м./сек.

За 1 секунду движущееся с этой скоростью точки пространства перемещается на расстояние Х₂=21894 м.   Значит, не достающееся для одновременности перемещение  DХ составляет:

 

                DХ  = Х₁ – Х₂  = 30000м – 21894м = 8106 м.

 

В таблице 2 приведены значения, рассчитанные по формуле (2.18) ускорения,  испытываемые объектами на поверхности земли в зависимости от радиуса R  и интервала времени   t

Таким образом, из вышеизложенного анализа одновременности, на примере околоземного пространства следует, что теория одновременности позволяет раскрывать механизм взаимодействия объектов друг с другом, находящихся на расстоянии в пространстве. В классической механике это взаимодействие называлось гравитацией. Все существующие в природе взаимодействия можно объединить, на общую основу, считая первопричиной  их    возникновения

 

Таблица 2

Показатели ускорения для достижения одновременности объекта

относительно центра Земли

Скорость начала отсчета м/сек:  30000			Скорость света:м/сек 300000000			Угловая скорость земли 0,000073
Радиус R	Интервал времени t	Скорость   одновре-менности м/сек		Переме-шение за 1 сек	Реальная скорость  поверхнос-ти земли		Соответ. перемеще-ние  за1 c 463,55*1/t	Резница перемещений	Ускорение
6350000	0,02116667	635		30000	463,55		21900	8100	9,811808
6345000	0,02115	634,5		30000	463,185		21917,26	8082,7423	9,817279
6340000	0,02113333	634		30000	462,82		21934,54	8065,4574	9,822819
6335000	0,02111667	633,5		30000	462,455		21951,85	8048,1452	9,828428
6330000	0,0211	633		30000	462,09		21969,19	8030,8057	9,834107
6325000	0,02108333	632,5		30000	461,725		21986,56	8013,4387	9,839856
6320000	0,02106667	632		30000	461,36		22003,96	7996,0443	9,845677
6315000	0,02105	631,5		30000	460,995		22021,38	7978,6223	9,85157
6310000	0,02103333	631		30000	460,63		22038,83	7961,1727	9,857534
6305000	0,02101667	630,5		30000	460,265		22056,3	7943,6955	9,863572
6300000	0,021	630		30000	459,9		22073,81	7926,1905	9,869683
6295000	0,02098333	629,5		30000	459,535		22091,34	7908,6577	9,875869
6290000	0,02096667	629		30000	459,17		22108,9	7891,097	9,882129
6285000	0,02095	628,5		30000	458,805		22126,49	7873,5084	9,888465
6280000	0,02093333	628		30000	458,44		22144,11	7855,8917	9,894878
6275000	0,02091667	627,5		30000	458,075		22161,75	7838,247	9,901367
6270000	0,0209	627		30000	457,71		22179,43	7820,5742	9,907933
6265000	0,02088333	626,5		30000	457,345		22197,13	7802,8731	9,914578
6260000	0,02086667	626		30000	456,98		22214,86	7785,1438	9,921302

одновременность взаимодействующих материальных объектов в едином пространстве–времени.

Осознание принадлежности нам, живущим на земле, только одновременной с нами окружающей природы и признание существования недоступных нашему наблюдению миров, является основным нововведением вносимой теорией одновременности в науку.  Для наблюдателя в пространстве, обозначены свои моменты: вчера, сегодня, завтра, через месяц, через год. Эти моменты абсолютны с точки зрения наблюдателя, т.е. их можно пережить только однажды. Последовательность моментов непрерывно в одной точке и, следовательно, требование непрерывной одновременности отдаленного окружающего связано с определенными условиями. Только выполняющие эти условия объекты окружающего одновременны наблюдателю на протяжении продолжительного времени. С точки зрения одновременности все наблюдаемые вокруг процессы и все измеряемые показатели,  такие как расстояние, время, масса, температура, плотность и др., считаются относительными и реальными для конкретного наблюдателя. Мы шагая по земле на 1 метр между двумя биениями сердца перемешаемся относительно центра земли примерно на 460 метров и можем измерить только то пространственное расстояние которое тоже перемешается на это расстояние. Перевод всех измеряемых показателей в ранг относительных значительно расширяет область изучаемых явлений и процессов. Вместе с этим, расширится наш круг понятий, касающихся окружающего мира. Весь ХХ век прошел поиском отличий относительных показателей от абсолютных и стремлением понять относительность.  Это стремление ограничивалось рамками независимого времени классической механики. К концу века движение фундаментальной физической науки остановилось, натолкнувшись с барьером независимой времени. Только перешагнув через этот барьер, науке третьего тысячелетия откроются новые, безграничные горизонты в научном познании окружающего мира.

 

 

С О Д Е Р Ж А Н И Е

       Введение.  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .   .   .  .  .  .  .  3

I.                       Одновременное, относительно  точки  наблюдения, пространство .  .  .  .   .  .  .  .  .     .   .  .   . 4 

II.   Условия соблюдения одновременности относительно движущейся точке  наблюдения  ..  .  . 13

 

ЛИТЕРАТУРА

 

1.      Бекжонов Р. Эйнштейн ва нисбийлик назарияси. Т., Укитувчи”.; 1978.

2.      Гулиа Н.В. Инерция. М.; Наука. 1982.

3.      Кори-Ниязов Т.Н. Астрономическая школа Улугбека. М.; Изд.АН.СССР, 1950.

4.      Самандаров Х.С. Исследования основ динамики движения с точки зрения сохранения энергии. Ургенч .”Хорезм”.1996.

5.      Самандаров Х.С. Физика движения во взаимосвязанном пространстве-времени. Ургенч .1999.

6.      Фейнман Р., Лейтон Р., Сендс М. Фейнмановские  лекции по физике. /пер.с англ. М.;Мир. 1976.

7.      Хайкин С.Э. Физические основы механики. М.;Наука. 1971.

8.      Эйнштейн А. “Научные труды” т.1-4. М.;Наука.1965.

 

ХОРЕЗМЕЦ - ХУРМАТ САБИРОВИЧ САМАНДАРОВ. ОДНОВРЕМЕННОСТЬ И ЕЕ РОЛЬ В  ПОЗНАНИИ ОКРУЖАЮЩЕГО  МИРА